Flow Matching 工程实践:从零实现 OT-CFM
这是一个从零开始实现最基础 Flow Matching (Naive Flow Matching) 的方法,基于Optimal Transport Conditional Flow Matching (OT-CFM) 路径来实现。
目标:训练一个模型,将标准高斯噪声(源分布)变换为 2D “双月” 数据(目标分布)。
核心思想回顾: 不需要复杂的 SDE 推导,我们只需要做三件事:
- 采样:取一个噪声点 $x_0$ 和一个数据点 $x_1$。
- 插值:在它们之间画一条直线,随机选一个时间 $t$,计算中间位置 $x_t$。
- 回归:训练神经网络在输入 $(t, x_t)$ 时,预测这条直线的方向(速度) $x_1 - x_0$。
环境准备
你需要安装以下库:
| |
第一步:准备数据 (Data Preparation)我们需要一个简单的 2D 数据集作为目标分布 $p_1$。这里使用 sklearn 的 make_moons。
| |
1. 数据集构建
| |
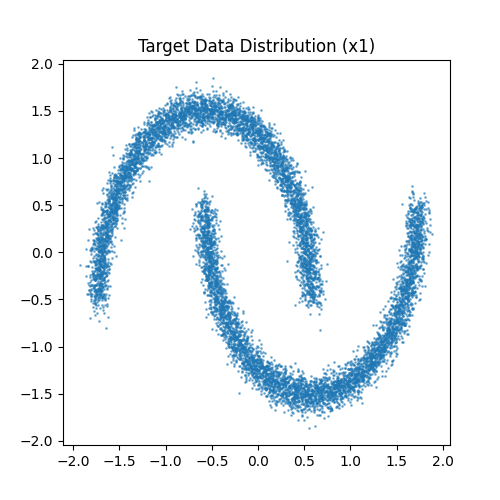
双月数据分布
第二步:搭建向量场网络 (The Vector Field Network)这是 Flow Matching 的核心模型 $v_\theta(t, x)$。它接收时间 $t$ 和位置 $x$,输出速度向量。输入:时间 $t$ (维度 1) + 坐标 $x$ (维度 2) = 3。输出:速度 $v$ (维度 2)。技巧:为了让网络更好地感知时间 $t$,我们不仅将 $t$ 作为输入,还可以使用简单的 Embedding(或者直接拼接,对于简单 2D 任务直接拼接即可)。
| |
第三步:构建 Flow Matching 损失函数 (The Crucial Step)这是工程实现中最关键的一步。根据文档中的 OT-CFM 公式:路径:$x_t = (1 - t)x_0 + t x_1$目标速度:$u_t(x|x_0, x_1) = x_1 - x_0$我们需要在代码中动态构建这个训练对。
| |
第四步:训练循环 (Training Loop) 把上面的部分组合起来进行训练。
| |
第五步:采样/推理 (Inference via ODE Solver)训练好模型后,我们得到了一个向量场。要生成数据,我们需要从噪声 $x_0 \sim \mathcal{N}(0, I)$ 出发,沿着向量场积分到 $t=1$。这本质上是解一个 ODE(常微分方程):
$$dx = v_\theta(t, x) dt$$为了教学目的,我们手写一个最简单的 欧拉求解器 (Euler Solver)。
| |
第六步:结果可视化 (Visualization) 最后,我们将生成的样本与真实分布对比,并画出粒子移动的轨迹,以验证 Flow Matching 是否成功学习了“直线”路径。
| |
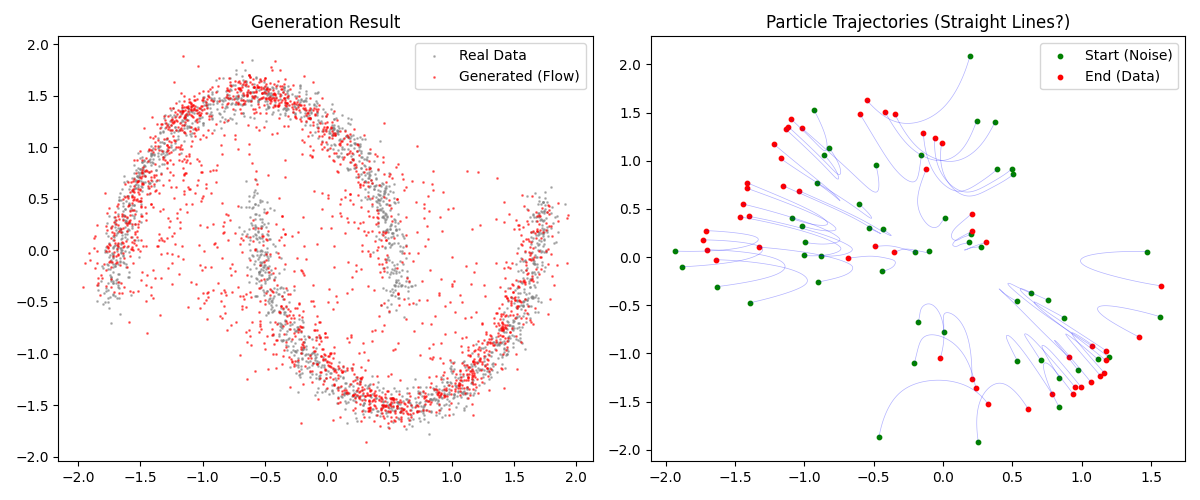
运行结果
这个教程实现了一个最简单的 Flow Matching 系统。在 Flow Matching (OT-CFM) 中,我们训练模型去逼近直线路径 ($x_1 - x_0$)。理想情况下,推理阶段的粒子轨迹应当是非常直的。这与扩散模型不同,扩散模型的逆向生成过程轨迹通常是弯曲且充满噪声的。轨迹越直,意味着我们可以用更大的步长(更少的 n_steps)来求解 ODE,这就是 Flow Matching 生成速度快的原因。代码关键点:Loss 计算:没有复杂的积分,仅仅是简单的 MSE 回归。时间输入:必须把 $t$ 喂给网络,因为向量场是随时间变化的 (Time-dependent)。
Simulation-Free:训练过程中我们没有调用 ODE 求解器,只在最后生成时调用了一次。你可以尝试将 n_steps 在 sample_euler 中减少到 10 甚至 5,你会发现效果依然不错,这展示了 FM 的鲁棒性。